Свойства степеней: описание, формулы, примеры

Еще в Древнем Египте использовались задачи на вычисление степеней. В этом был практический смысл, ведь папирус стоил дорого, а перемножать приходилось большие числа, вот и придумали древние египтяне, как проводить вычисления и одновременно экономить место (1). Каковы же свойства степеней с точки зрения современной математики? Рассмотрим их вместе с преподавателем.

Что такое степень числа в алгебре

Степенью числа в алгебре называется математическая операция, представляющая собой многократное умножение числа на само себя. Главными элементами степени числа являются: основание (число, умноженное само на себя) и показатель (натуральное число, равное количеству операций умножения).

3 = 3×3×3×3×3 = 243.

Бывают следующие особые случаи, характерные для степени числа:

1. Нулевая степень: a = 1 (для a ≠ 0).

2. Первая степень: a = a.

3. Единица в степени: 1 = 1.

4. Ноль в степени: 0 = 0 (для n > 0).

Свойства степеней с натуральными показателями

Степени с натуральными показателями обладают рядом важных свойств. Рассмотрим их более подробно вместе с формулами и примерами.

Умножение степеней с одинаковыми основаниями

В случае умножения степеней с одинаковыми основаниями, основания остаются без изменений, а показатели степеней складываются.

Формула:

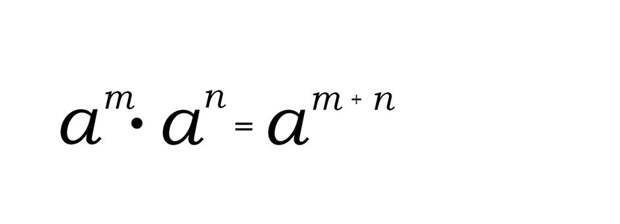
Пример:

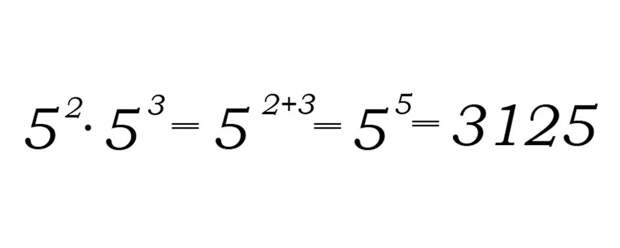
Деление степеней с одинаковыми основаниями

Если происходит деление степеней с одинаковыми основаниями, то основания остаются те же, а показатели степеней вычитаются.

Формула:

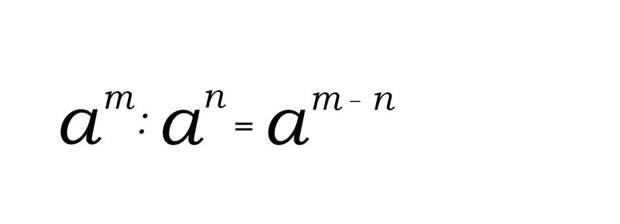
Пример:

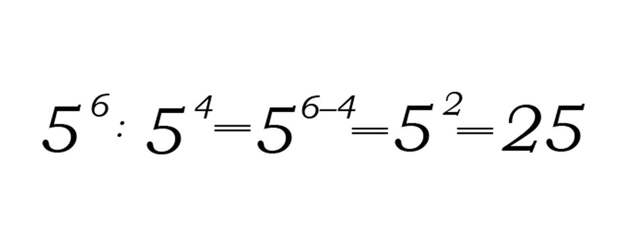
Возведение степени в степень

При возведении степени в степень основание степени остается без изменения, а показатели степеней перемножаются.

Формула:

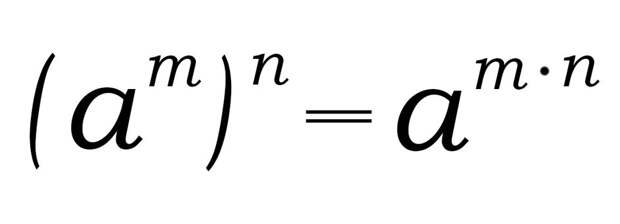
Пример:

Возведение в степень произведения

Когда возводится в степень произведение, вначале каждый из множителей возводится в степень, а затем полученные результаты перемножаются.

Формула:

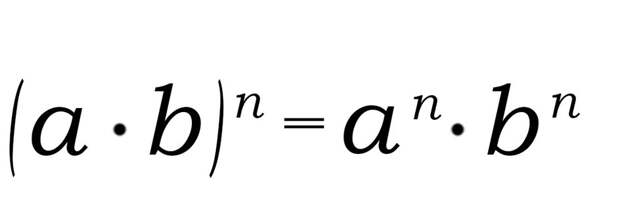
Пример:

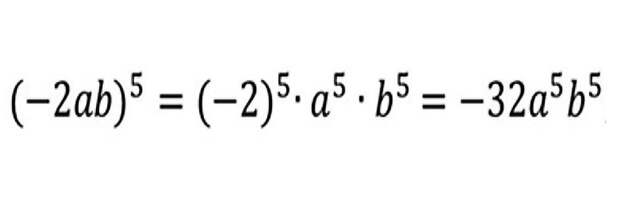
Возведение в степень частного

Для возведения в степень частного следует возвести в эту степень отдельно делимое и делитель, а потом первый результат разделить на второй.

Формула:

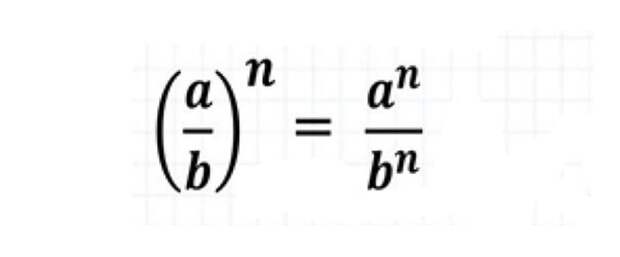
Пример:

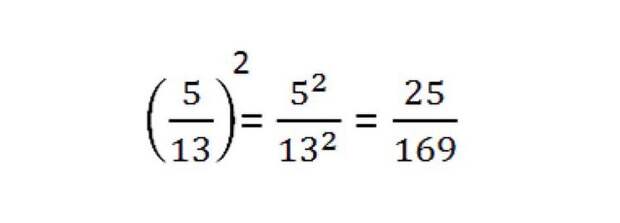
Свойства степеней с рациональными показателями

Рассмотрим основные свойства степени с рациональным показателем.

Умножение степеней с дробью

Для умножения дробных степеней с одинаковыми основаниями следует основания оставить без изменений, а показатели степеней суммировать.

Формула:

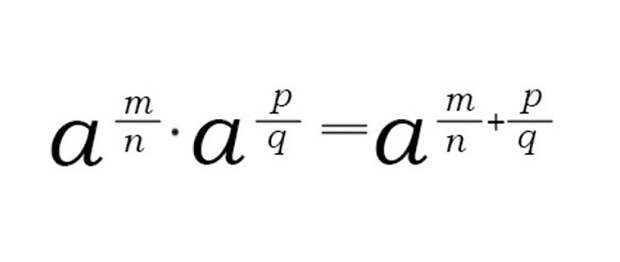
Пример:

Деление степеней с дробью

При делении дробных степеней с одинаковыми основаниями основания остаются те же, а показатели степеней вычитаются.

Формула:

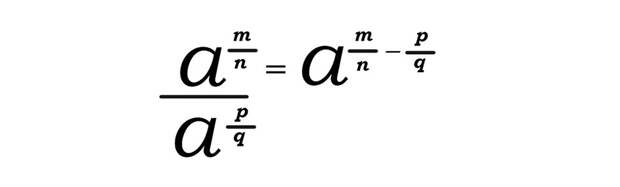
Пример:

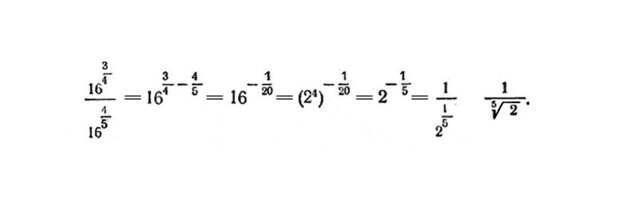
Возведение степени в степень с дробью

В случае возведения дробной степени в степень основание степени остается без изменения, а показатели степеней перемножаются.

Формула:

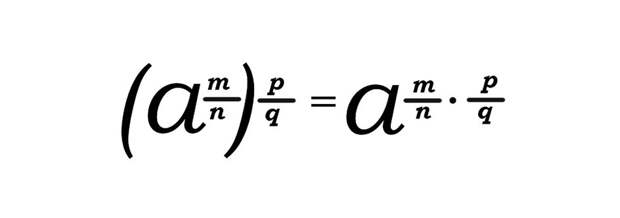
Пример:

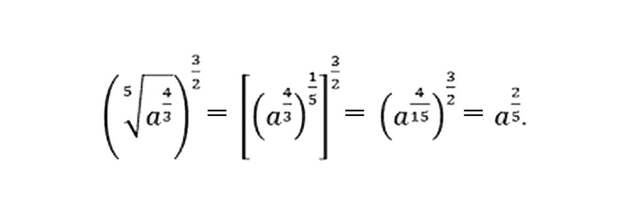
Возведение в степень произведения с дробью

При возведении в степень произведения с дробью, вначале каждый из множителей возводится в степень, а затем полученные результаты перемножаются.

Формула:

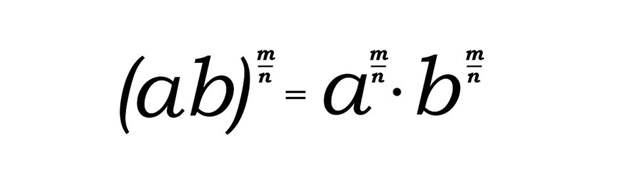
Пример:

Возведение в степень частного с дробью

Для возведения в степень частного с дробью нужно возвести в эту степень отдельно делимое и делитель, а потом первый результат разделить на второй.

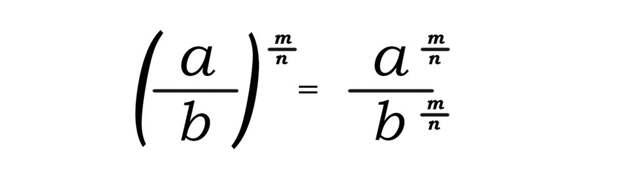
Пример:

Почему свойства степеней изучают в 7-м классе

К седьмому классу у школьников уже достаточно развиты базовые навыки работы с умножением и делением, что позволяет переходить к изучению степеней. Эта тема, в свою очередь, является основой для понимания линейных и квадратных уравнений, логарифмов и математического анализа, изучаемых в старших классах.

«В седьмом классе математика, изучаемая в 1−6 классах, переходит на новый уровень и трансформируется в алгебру, геометрию и вероятность и статистику. Основная часть материала в разделе “Алгебра” посвящена изучению различных методов манипуляции с выражениями. Свойства степеней становятся ключевыми инструментами в решении уравнений и упрощении выражений, позволяя учащимся выполнять более сложные вычисления с переменными и константами.

Изучение свойств степеней в 7 классе неслучайно, ведь это время, когда учащиеся начинают понимать, что математика — это не просто набор правил, а целая система взаимосвязей. Свойства степеней, такие как произведение степеней с одинаковыми основаниями, деление степеней и возведение в степень, образуют фундамент для более сложных математических тем. Эти свойства используются не только в алгебре, но и в других разделах математики, например геометрии и далее в курсе анализа, который изучается в старших классах«, — поясняет Анна Жадан, старший преподаватель математики Домашней школы «ИнтернетУрок».

Мнение эксперта

Рассказать, для чего используются свойства степеней, мы попросили нашего эксперта Анну Жадан. Вот ее профессиональное мнение:

"Использование свойств степеней позволяет значительно упростить вычисления, облегчить работу с алгебраическими выражениями и решать более сложные задачи, с которыми сталкиваются ученики, студенты и профессионалы.

Во-первых, свойства степеней помогают упростить вид многочленов и дробно-рациональных выражений. Используя такие свойства, ученики могут превращать сложные выражения в более простые формы, что делает их более удобными для последующей работы.

Во-вторых, свойства степеней играют ключевую роль в решении уравнений. Многие алгебраические уравнения, особенно те, которые содержат переменные в степени, требуют использования правил работы со степенями для нахождения корней.

Свойства степеней также играют важную роль в анализе функций. Решая такие задачи, ученики сталкиваются с необходимостью манипулировать степенями, чтобы провести исследование поведения функций. Это знание является основополагающим для более поздних тем в математике, таких как производные и интегралы.

Кроме того, свойства степеней активно используются в прикладной математике, физике и инженерных науках".

Что нужно запомнить о степени числа и ее свойствах

Перечислим еще раз главные положения статьи.

• Степень числа — это математическая операция, заключающаяся в многократном умножении числа на само себя.
• Основание степени числа — число, умноженное само на себя.
• Показатель степени числа — натуральное число, равное количеству операций умножения.
• Свойства степеней изучают в 7-м классе, так как к этому времени у учащихся уже достаточно развиты базовые навыки работы с умножением и делением.
• Тема «Свойства степеней» является основой для понимания логарифмов, линейных и квадратных уравнений, математического анализа, изучаемых в старших классах.

Источник:

Гильмуллин М. Ф. «История математики: Учебное пособие. Елабуга». 2012.