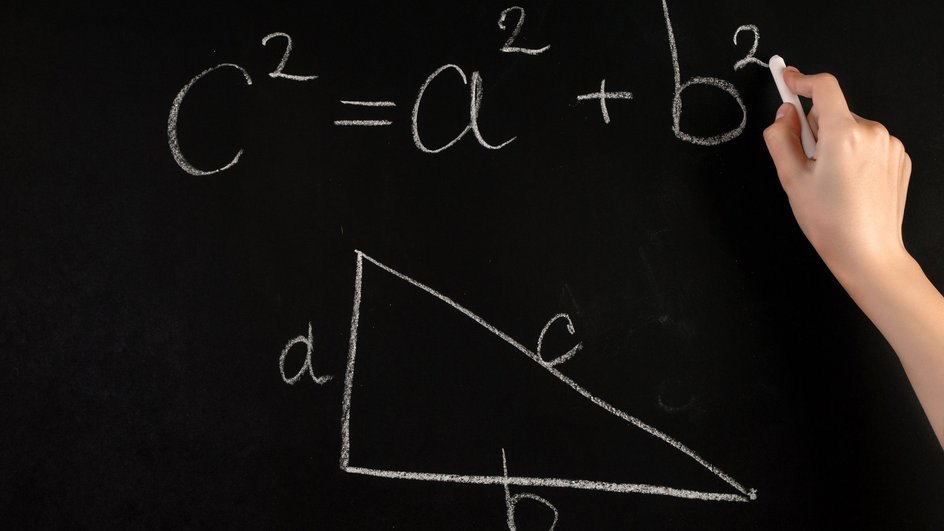
Одна из самых известных и важных теорем в математике помогает понять взаимосвязь между сторонами прямоугольного треугольника. Рассказываем, кто такой Пифагор, как работает его теорема, а также рассматриваем несколько практических примеров.
Кто такой Пифагор
Это древнегреческий ученый и философ, создатель школы пифагорейцев и автор множества научных открытий. О его жизни сохранилось множество легенд и совсем мало точных фактов.
Идеи Пифагора оказали огромное влияние на развитие науки в целом и математики в частности. Например, он создал учения о подобии геометрических фигур, построении правильных многоугольников и прямолинейных фигур, четных и нечетных числах и многие другие теории и доказательства.
Философу также присваивают авторство известной теоремы о соотношении сторон в прямоугольном треугольнике. На самом деле она была известна задолго до Пифагора. Например, древние египтяне знали, что треугольник со сторонами 3, 4 и 5 является прямоугольным, и использовали его параметры при построении зданий и межевании земель (1).
О чем гласит теорема Пифагора: суть простыми словами
Каждый прямоугольный треугольник состоит из трех сторон, которые носят отдельные названия. Сторона, лежащая напротив прямого угла, называется гипотенузой. Линии, которые пересекаются под углом 90°, — катетами.
Формула теоремы Пифагора
Если обозначить катеты a и b, а гипотенузу — c, получится следующая формула:
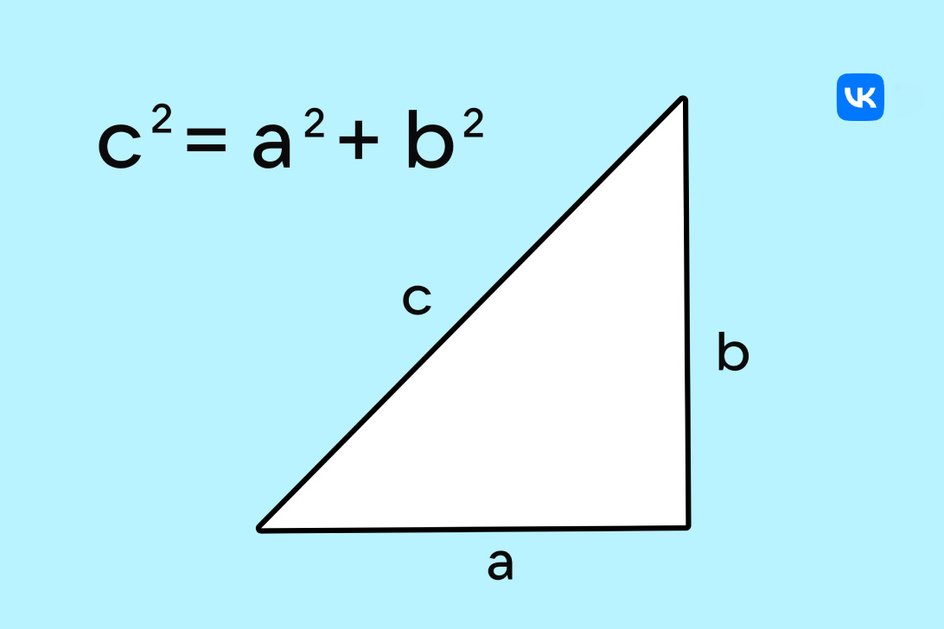
Из теоремы можно вывести еще несколько математических соотношений:
с = a²+b²
2. Для нахождения одного из катетов:
a = c²-b²
b = c²-a²
Доказательство теоремы Пифагора
Сегодня существует более 300 различных доказательств известного утверждения. Мы приведем несколько самых известных. За основу возьмем треугольник ABC с катетами a, b и гипотенузой c.
Геометрическое доказательство с квадратами
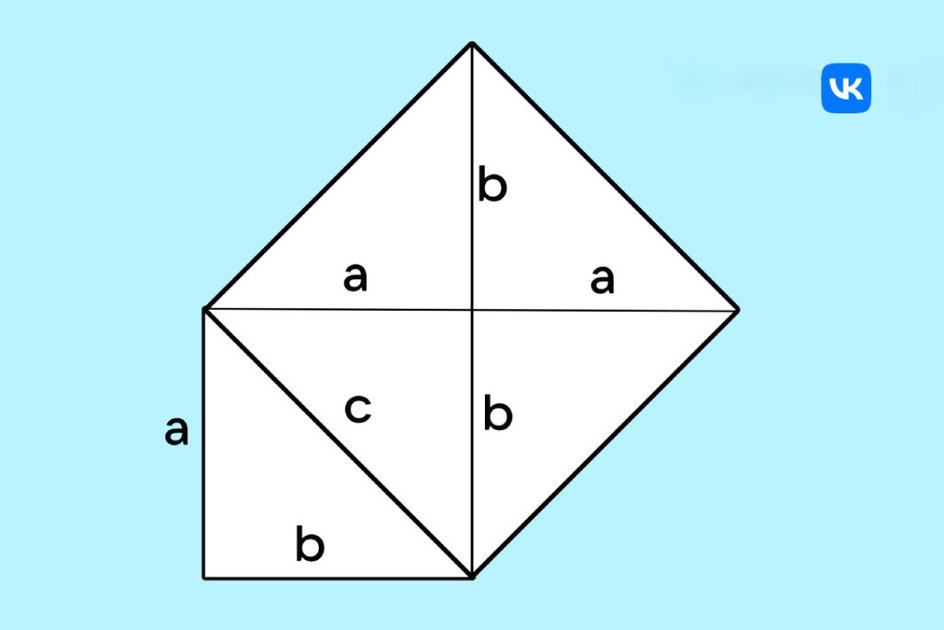
Построим на гипотенузе треугольника квадрат со стороной c. Внутри него разместим четыре одинаковых прямоугольных треугольника, у каждого из которых будут катеты a и b. Эти треугольники будут расположены так, что образуют внутренний квадрат со стороной (b – a).
Площадь большого квадрата равна c², а площадь четырех треугольников: 4 × ½ab = 2ab.
Тогда площадь внутреннего квадрата равна (b – a)².
Таким образом, можно записать равенство площадей:
c² = 4 × ½ab + (b – a)².
Если раскрыть скобки и упростить пример, получится: a² + b² = c².
Алгебраическое доказательство
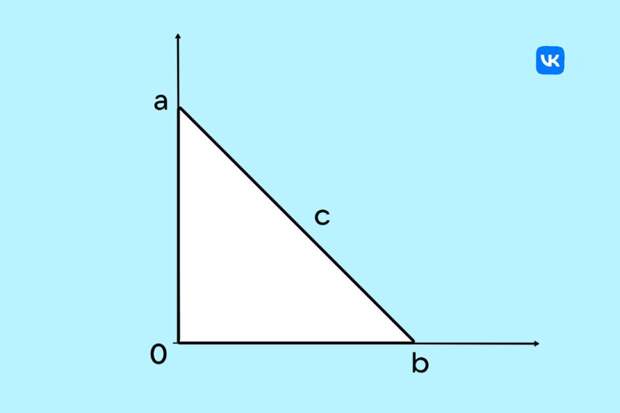
Разместим наш треугольник на системе координат: один катет будет совпадать с осью x, а другой — с осью y. Координаты вершин будут: (0, 0), (a, 0), (0, b).
Длину гипотенузы можно найти по формуле расстояния между двумя точками (3):
c = √((a – 0)² + (0 – b)²) = √(a² + b²).
Если возведем обе стороны в квадрат, получим:
c² = a² + b²
Доказательство с помощью подобия треугольников
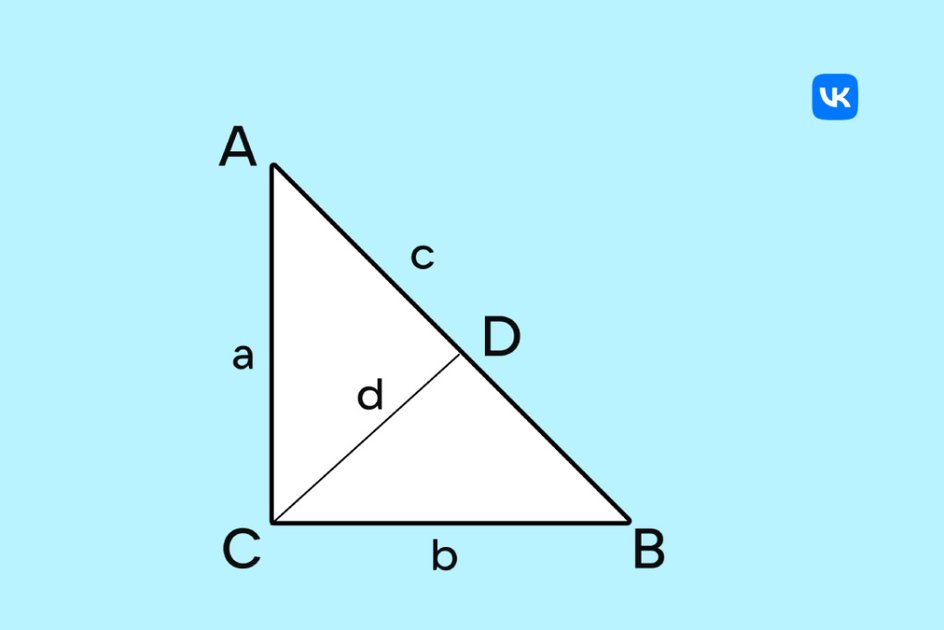
Проведем высоту CD из вершины C на гипотенузу AB. Получатся два меньших прямоугольных треугольника ADC и BDC, которые подобны исходной фигуре.
По теореме о свойствах подобия треугольников можно вывести следующее соотношение:
a/c = d/a и b/c = d/b,
где d — высота CD.
Из этих соотношений получаем:
- d = a²/c
- d = b²/c.
Приравнивая два выражения для d и умножая на c, получаем:
a² + b² = c².
О чем гласит обратная теорема Пифагора
В геометрии также существует перевернутая версия известного утверждения, или теорема Пифагора для обратных величин.


Формула и доказательство обратной теоремы Пифагора
В основе утверждения лежит та же известная формула: a² + b² = c².
Если в треугольнике со сторонами a, b и c выполняется условие a² + b² = c², то один из углов равен 90°.
Доказательство теоремы приводит Дарья Дейген, эксперт ЕГЭ, преподаватель математики, заместитель директора Университетской гимназии МГУ:
— Рассмотрим треугольник со сторонами 3, 4 и 5. Подставим длины в выражение a² + b² = c². Получим:
52 = 42 + 32
25 = 16 + 9
25 = 25
Примеры задач с теоремой Пифагора
Эту тему изучают на уроках геометрии в восьмом классе. Приведем несколько задач с теоремой Пифагора, чтобы научиться правильно применять формулу.
Найти гипотенузу
Условие: прямоугольный треугольник с катетами, равными 12 и 35 см. Найдите длину гипотенузы.
Решение:
Используем теорему Пифагора: a² + b² = c²
Подставим значения катетов и решим пример:
(12 × 12) + (35 × 35) = 144 + 1225 = 1369
√1369 = 37
Ответ: гипотенуза равна 37 см.
Найти катет
Условие: в треугольнике одна сторона равна 6 см, а гипотенуза — 10 см. Найдите длину второго катета.
Пусть длина второй стороны — b.
По теореме Пифагора:
10² = 6² + b²
100 = 36 + b²
b² = 100 – 36 = 64
Следовательно:
b = √64 = 8 см
Ответ: длина катета равна 8 см.
Задача на обратную теорему Пифагора
Условие: в треугольнике одна сторона равна 5 см, а другая — 12 см. Является ли этот треугольник прямоугольным?
Решение:
Проверим по обратной теореме Пифагора. Пусть гипотенуза — c:
c² = 5² + 12² = 25 + 144 = 169
c = √169 = 13 см
Так как сумма квадратов катетов равна квадрату гипотенузы, этот треугольник является прямоугольным.
Пифагоровы тройки
— Это наборы из трех целых положительных чисел, которые удовлетворяют уравнению теоремы Пифагора, — объясняет эксперт Дарья Дейген.
Приведем некоторые пифагоровы тройки в таблице.
| a (катет) | b (катет) | c (гипотенуза) |
| 3 | 4 | 5 |
| 5 | 12 | 13 |
| 8 | 15 | 17 |
| 7 | 24 | 25 |
| 9 | 40 | 41 |
| 12 | 35 | 37 |
| 13 | 84 | 85 |
| 16 | 63 | 65 |
| 20 | 21 | 29 |
| 20 | 99 | 101 |
| 28 | 45 | 53 |
| 33 | 56 | 65 |
| 36 | 77 | 85 |
| 39 | 80 | 89 |
Мнение эксперта
— Теорема Пифагора гласит, что в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов, — уточнила Дарья Дейген. — Разберем это утверждение подробнее. В прямоугольном треугольнике один угол прямой, то есть равен 90°. Сторона, лежащая напротив прямого угла, называется гипотенузой. Это самая длинная сторона в прямоугольном треугольнике. Две другие называются катетами.
c² = a² + b²
— Чтобы ускорить вычисления, полезно помнить про пифагоровы наборы чисел и использовать таблицы с ними в школе, — советует эксперт.
Что нужно запомнить о теореме Пифагора
Эта простая формула помогает решить много практических задач и научиться лучше разбираться в геометрии. Собрали основную информацию про теорему Пифагора:
- О соотношении сторон в прямоугольном треугольнике было известно с древних времен. Математик и философ Пифагор доказал, что в такой фигуре сумма квадратов катетов равна квадрату гипотенузы.
- Формула теоремы Пифагора: c² = a² + b²
- Обратное утверждение тоже верно: если в каком-либо треугольнике квадрат одной стороны равен сумме квадратов двух других сторон, то такой треугольник — прямоугольный.
- Три натуральных числа, которые подходят под условия теоремы Пифагора, называются пифагоровой тройкой. Их используют, чтобы ускорить решение задачи.
Список источников:
- Глейзер Г. О теореме Пифагора и способах ее доказательства. Математика, № 24. 2001.
- Диоген Лаэртский. О жизни, учениях и изречениях знаменитых философов. Под ред. А. Лосева. 1979.
- Яковлев И. Материалы по математике.
Эксперт: Дарья Дейген, эксперт ЕГЭ, преподаватель математики, заместитель директора Университетской гимназии МГУ
Свежие комментарии